How Machines Learn to Write
From Shannon’s prediction game to modern transformers—and what gets lost in meaning
The Mysteries of Words
A few years ago, I sat in a dissertation defense for a student working on language models, and something quietly unsettled me. He was explaining “attention mechanisms,” showing how his system could summarize documents in perfect English. I remember watching the examples scroll by, line after line, unlike earlier machine-generated texts, carrying no seams.
After the defense, there was a small celebration. Over coffee and cake, I asked colleagues where this whole idea had begun. Someone mentioned ELIZA: the first chatbot that simulated conversation. ELIZA’s famous DOCTOR script mimicked a psychotherapist, reflecting users’ words back at them and so creating the illusion of understanding.
It didn’t have a model of meaning; it was based on pattern-matching and substitution. And yet many people responded as if it did. That strange human tendency to attribute feeling to a simple program was later called the ELIZA effect. Curious, I traced the thread further back and realized that ELIZA stood on a foundation laid much earlier by Alan Turing. Turing had, in fact, written two remarkable papers just after World War II.
In 1948, in “Intelligent Machinery”, he sketched what he called an “unorganized machine,” a crude model of the infant brain. Its wiring was initially random, but through reward, punishment, and random exploration, it could be “educated” into a universal computer. To prove its worth, he proposed a set of benchmark tasks: games like chess and cryptography as easier challenges, mathematics and translation as harder ones, and at the very top, the learning of natural language. Already, he sensed that teaching a machine language would be the ultimate test.
Two years later, in 1950, in “Computing Machinery and Intelligence”, he posed his famous provocation: not “Can machines think?” but whether they could succeed in the imitation game, what we now call the Turing Test. Once again, language was the centerpiece. He imagined training a machine as one might teach a child, through interaction, naming, and correction.
In hindsight, ELIZA was almost a toy realization of Turing’s challenge: a machine producing conversation that, for some, passed as human. It was a small step, but a definitive one on the march toward what we now call artificial intelligence. That was the lineage: from Turing, through ELIZA, to the models I had just seen.
The resemblance was striking, but also disorienting. It blurred the boundary between words that merely followed rules and words that carried meaning. The harder task was never finding the words, but shaping the essence they had to carry. Unlike the demo I saw, which simply strung together the most probable words, I faced a different kind of struggle: I knew the words, but the felt essence wasn’t there yet. That quiet, internal wrestling, the pause and reshaping before meaning lands, was absent in the polished texts before me.
This is not merely a technical matter of algorithms. Language is bound up with social practice, with the rituals and repositories by which communities make sense of the world. A sentence does more than map signs to ideas; it declares, commands, consoles, jokes, curses, remembers, and binds people together in common projects. Across cultures and centuries, in oral performance and written text, language accumulates authority and history: it carries law, theology, love letters, treaties, protests, prayers, jokes, and recipes.
I grew up with the Ramayana and the Mahabharata, not as entertainment but as living traditions: vast conversations full of moral dilemmas, strategic debates, and philosophical inquiry. The Bhagavad Gita, nested inside the Mahabharata, is itself a dialogue about duty and liberation that still guides millions. Later, in English, I discovered Shakespeare’s soliloquies and the playful wit of Pygmalion. Across these forms, language is never merely syntax or sequence; it is a vessel through which thought, memory, and moral imagination endure.
But language is not the only such vessel. Music can convey emotion more directly than a sentence. A painting can express what words cannot. Athletes speak through rhythm and gesture; mathematicians through symbols and proof. These are all languages in a broader sense: systems of signs that carry meaning.
What sets natural language apart is its paradoxical combination of simplicity, fragility, and reach. Compared to music, it is a sparse medium. Just strings of symbols. And that simplicity makes it radically fragile: a comma, a tense, or a single word can tilt the whole meaning. Yet because it can describe, question, command, or console, its coverage is unmatched. Perhaps this is why Turing placed language at the pinnacle of machine intelligence: to master something so lean, so delicate, and so general would be to master almost anything.
That ambition, once only theoretical, suddenly felt realized when ChatGPT arrived. What had once been a curiosity in labs and conference rooms suddenly erupted into daily life. A seminar-room marvel became a household word. Classrooms, newsrooms, law firms, and living rooms all found themselves confronted by a machine that could speak in polished paragraphs. Students turned in assignments written by it, professionals drafted memos with it, and friends sent poems and prayers through it. Headlines proclaimed that human thought itself had been hacked.
The effect was electric, unsettling, and irresistible: a machine producing not just a clever reply but a torrent of fluent language on command: text that could mimic styles, explain theories, or console in grief. Where earlier chatbots exposed their seams within a few exchanges, this one could sustain entire conversations, sounding by turns confident, witty, or wise. For many, it felt like crossing a threshold: as if the capture of language, the vessel of our thought, memory, and imagination, had also led to the capture of thought itself.
But had it?
Shannon and the Probability of Language
To understand what today’s language models are really doing, we have to return to 1948. That year, Claude Shannon published “A Mathematical Theory of Communication”, the paper that founded information theory. Shannon and Turing overlapped at Princeton; their landmark papers appeared two years apart but, interestingly, didn’t cite each other. Two giants, side by side, glimpsed the same radical possibility: that thought, conversation, even language itself could be treated as a process of symbols and probabilities.
I first encountered Shannon’s paper much later, during my own Ph.D. At the time, my attention was on the mathematics: entropy, channels, error-correcting codes. His playful examples with English text felt like curiosities, illustrations at the edge of a serious theory. Only years later did I realize that those throwaway examples were the key: they pointed to a new way of thinking about language itself.
Shannon didn’t just write equations; he showed that English itself could be reduced to probabilities. He built little “English-like” texts by choosing letters and words at different levels of approximation.
At the crudest level, just picking letters at random, the result was nonsense:
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ…
Add a bit of structure, and things improve. Choose letters in proportion to their frequency in English, and the sequences at least look more English-like. Let each letter depend on the one before, and fragments of words begin to appear:
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID…
Finally, move up to whole words, chosen by likelihood, and the result is uncanny:
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE…
The sentences don’t mean anything, but they feel eerily English. Already here, the paradox is clear: the surface of language can be conjured from probabilities, yet the interior—intention, resonance, meaning—remains absent. The game of continuation can mimic the sound of thought without ever touching its substance. This is precisely why those examples felt like mere curiosities when I first encountered them during my Ph.D.
Shannon’s insight replaced semantic complexity with statistical clarity. Friction was no longer a feature; it became noise to be eliminated. This choice, language as probability rather than lived expression, is the path today’s models still follow.
But it’s worth pausing to note: this path is very different from the one that later revolutionized images through diffusion models. Diffusion works by adding and then removing noise in a smooth, continuous space of pixels. Language doesn’t live in such a space. Its basic units: words, subwords, and characters are discrete symbols, and you can’t nudge them the way you can blur or sharpen an image. That’s why language models followed a different road: prediction, not denoising. I’ll return to this contrast later, but for now, it’s important to see why prediction became the natural engine of machine language.
This was the first glimpse of what we now call autoregressive models: a model producing fluent text by following the statistical trail of past patterns. It was only a hint, a statistical seed that would grow into models built not on meaning, but on counting.
From Counting to Learning: The Statistical Road to Fluency
The formal idea behind it is simple: treat a sentence as a chain of chances (or probabilities). The chance of the full sentence is the chance of the first word, multiplied by the chance of the second word given the first, multiplied by the chance of the third word given the first two, and so on, word by word. If you can estimate those next-word chances, you can both score sentences and generate them.
Counting to Predict
The first way to estimate those chances was to count. Take a large collection of text: books, news, transcripts, and tally how often words follow one another. These counts become the raw material for what came to be called an n-gram model.
Look at words one by one (unigrams), and you learn that the is the most common word, followed by of and and. Look at words in pairs (bigrams), and short phrases emerge: of the, in the, to the. Extend to triples (trigrams), and you start to see fragments of longer phrases: once upon a, at the end, as soon as.
The model itself is nothing more than a table of probabilities: given the last n–1 words, what word most often comes next?
Training in this model is just tallying frequencies. Imagine your corpus contains the sentence:
The cat sat on the mat.
Each time you see the cat, you record that it is followed by sat. If you also find the cat ran, you note that too. Over time, the model builds up probabilities: after the cat, sat might have probability 0.67, ran 0.33.
Once trained, generation is just the Shannon continuation game:
Start with a seed word, say the.
Look at all words that follow the in your table.
Pick one, weighted by its probability, perhaps cat.
Now continue: after the cat, the most likely word is sat.
Word by word, the sentence grows.
This simple recipe could yield text that flowed with surprising smoothness. But the seams showed quickly: ask it to continue The cat sat on the kitchen… and it stalls. If that exact phrase never appeared in training, the model is lost. It cannot reason that floor would be a plausible continuation. It parrots patterns, but it cannot generalize.
Still, for all their brittleness, n-grams proved useful. They powered the first generation of statistical speech recognition systems, helped search engines rank documents, and even corrected spelling. If you typed I went too the stor, a bigram model could see that went to is far more probable than went too, and that the store is common, while the stor is not. The correction fell out of counts, not meaning.
In fact, in my job at IBM Research, I used n-gram models to solve customer problems of this kind. I didn’t see them as language generators; they were handy probabilistic tools. But their limits were obvious, and those limits are what pushed the field past counting.
Learning to Predict
The lesson from n-grams was right: you can generate text by guessing what comes next. The problem was how those chances were computed. Counting memorizes fragments in the dataset and is unable to generalize and generate new ones. The next idea was to use data to learn the probabilities rather than counting them.
In a learning autoregressive model, the next-word probability is no longer read from a table of counts. It comes from a function with many adjustable “knobs”: the model’s internal weights. Training means turning those knobs so that the function gives higher scores to the right word and lower scores to the wrong ones.
The process looks like this:
Take a sentence from your training data: The cat sat on the mat.
Hide the last word. The model is asked: Given “The cat sat on the,” what word should come next? The correct answer is mat.
Next, cover up the fifth word. Ask: Given ‘The cat sat on,’ what word comes next? Answer: the.
Do this for every position, across billions of sentences.
Each time the model makes a guess, it compares its guess with the actual word, adjusts its internal weights, and tries again. Over time, it learns to assign high probability to words that are correct continuations (among the examples it has seen), and lower probability to words that don’t fit.
This training process is nothing exotic. It’s a form of supervised learning we saw here. The input is a prefix of a sentence; the label is the next word. The dataset is simply a giant collection of sentences. The objective is to minimize prediction error.
But here’s the catch: functions only work on numbers. Words themselves are symbols, not numbers. So the first step is to convert each word into a numerical vector, an embedding.
And what happens once every word is a vector? Suddenly, the model can do geometry. It can combine the vectors of the words it has already seen to form a “context vector”: a kind of numerical fingerprint of the story so far. Then, it compares this context vector with the vectors of all possible next words. If the context lines up closely with fascinating, the score for fascinating will be high; if it lines up less well with boring, the score will be lower.
This is the crucial difference from n-grams. Instead of looking up “the cat sat on the …” in a brittle counting table, the model is asking a geometric question: which next word lies closest to the context in this space of embeddings?
That’s how autoregression becomes learning: by turning words into numbers, placing them in a map, and using geometry instead of counting to guess what comes next. Which leaves the question: how do we build such a map of words, a geometry rich enough to capture meaning?
Embedding Words in Continuous Spaces
The simplest idea is to assign each word a unique position in a very long list: one index per word. Since English has hundreds of thousands of words (some dictionaries put the number well over 200,000), the list is massive. You might let cat be position 27, dog 28, philosophy 3,102. The numbering is arbitrary; cat could just as well have been 5,000. In vector form, cat becomes [0, 0, 1, 0, 0, …], with a single “1” marking its location and every other slot set to zero. This representation makes words easy to distinguish, but the geometry is meaningless: cat is just as far from dog as from philosophy.
A more refined idea is to let experience shape the numbers. If two words often appear in similar surroundings, maybe they should be placed close together. Imagine plotting words on a map so that proximity reflects similarity, not by fiat but by usage.
Take a toy dataset of six sentences: The cat sat on the mat. The dog sat on the rug. The cat chased the puppy. The dog chased the puppy. The puppy played with the cat. The puppy played with the dog. If we track just a handful of features—mat, rug, puppy, chased, played—each word can be represented by how often it appears near them. In this scheme, cat becomes [1, 0, 2, 1, 1] (once near mat, twice near puppy, once near chased, once near played). Dog becomes [0, 1, 2, 1, 1] (once near rug, twice near puppy, once near chased, once near played). Sat, by contrast, is [1, 1, 0, 0, 0], tied mainly to mat and rug.
Even in this miniature world, geometry begins to show meaning. Cat and dog land close together because they share strong ties to puppy, chased, and played, while sat falls into a different region, bound to places rather than animals. What emerges is the first glimmer of semantic structure: words with similar contexts drift toward each other, forming clusters that hint at categories: animals here, actions there. But similarity is not the same as meaning: geometry can group, but it cannot ground.
Scaled up, every word becomes a learned vector in a high-dimensional space. Words in similar contexts cluster together. These positions aren’t assigned by hand; they emerge from data. This is the heart of embeddings: a flexible geometry that enables generalization.
This is where the machine’s world and ours begin to diverge: for it, closeness in space is enough; for us, meaning always carries history and intention.
Figure 1. Toy word embeddings. Words that appear in similar contexts (like “cat” and “dog” or “truth” and “meaning”) are drawn closer in a geometric space.
Once each word is embedded as a vector, the model can begin to play its guessing game. Take the phrase “The book was …” The vectors for the, book, and was are combined into a single context vector, a kind of numerical fingerprint of the story so far.
Now the model faces a choice. In principle, any word in the vocabulary could come next. To decide, it compares the context vector with the stored embeddings for each possible word. If it aligns closely with fascinating, the score for fascinating will be high. If it fits less well with boring or useful, their scores will be lower.
Training nudges these scores in the right direction. If the true next word is fascinating, the model is penalized for underestimating it. The error flows backward, adjusting the context and word vectors so that next time, fascinating aligns more strongly with book. Over billions of such corrections, the geometry of the space reshapes itself until the model mirrors the structure of language with uncanny fluency.
This shift, from rigid indexing to learned geometry, is what enables language models to generalize. They no longer rely on fixed mappings; they learn to navigate a space where distance encodes meaning, and calculus becomes a natural tool.
Interlude: Why Diffusion is Hard for Text
At this point, especially if you’ve read my earlier essay on diffusion models, you might wonder: if words now live in a continuous space, why not use the same methods that revolutionized images, like diffusion? After all, in images, you can corrupt a picture with a bit of Gaussian noise, then learn to reverse the process. Denoising works because pixels live in a continuous space; small perturbations still look like the same picture.
Language, however, resists this trick. Even though embeddings give us geometry, not every point in this space corresponds to a real word. You can move cat slightly toward dog, but halfway in between lies a meaningless vector. It doesn’t decode to anything.
This creates three obstacles:
No smooth corruption. Replace cat with cap, and the meaning shifts. Replace it with qat, and you fall out of the dictionary. There’s no gradual blur.
Semantic fragility. In images, small changes rarely flip meaning. In text, one word can invert it entirely: will vs. will not.
Combinatorial explosion. A diffusion model over text would need to account for every possible substitution at every position, an exponential blowup.
Even with geometry, language resists denoising. Prediction, not denoising, remained the natural path.
This brings us to transformers. Once words live in embeddings, the challenge becomes: how can a model attend to not just the last few words, but to whole paragraphs and documents?
Transformers: From Prediction to Attention
With embeddings in place, autoregression offered the right principle: language can be generated word by word by predicting what is most likely to come next. But early autoregressive models, like n-grams, were shallow and forgetful. They could only look back a short distance. If a key idea was more than a few steps behind, the model stumbled.
Yet language is full of long-range dependencies. Consider:
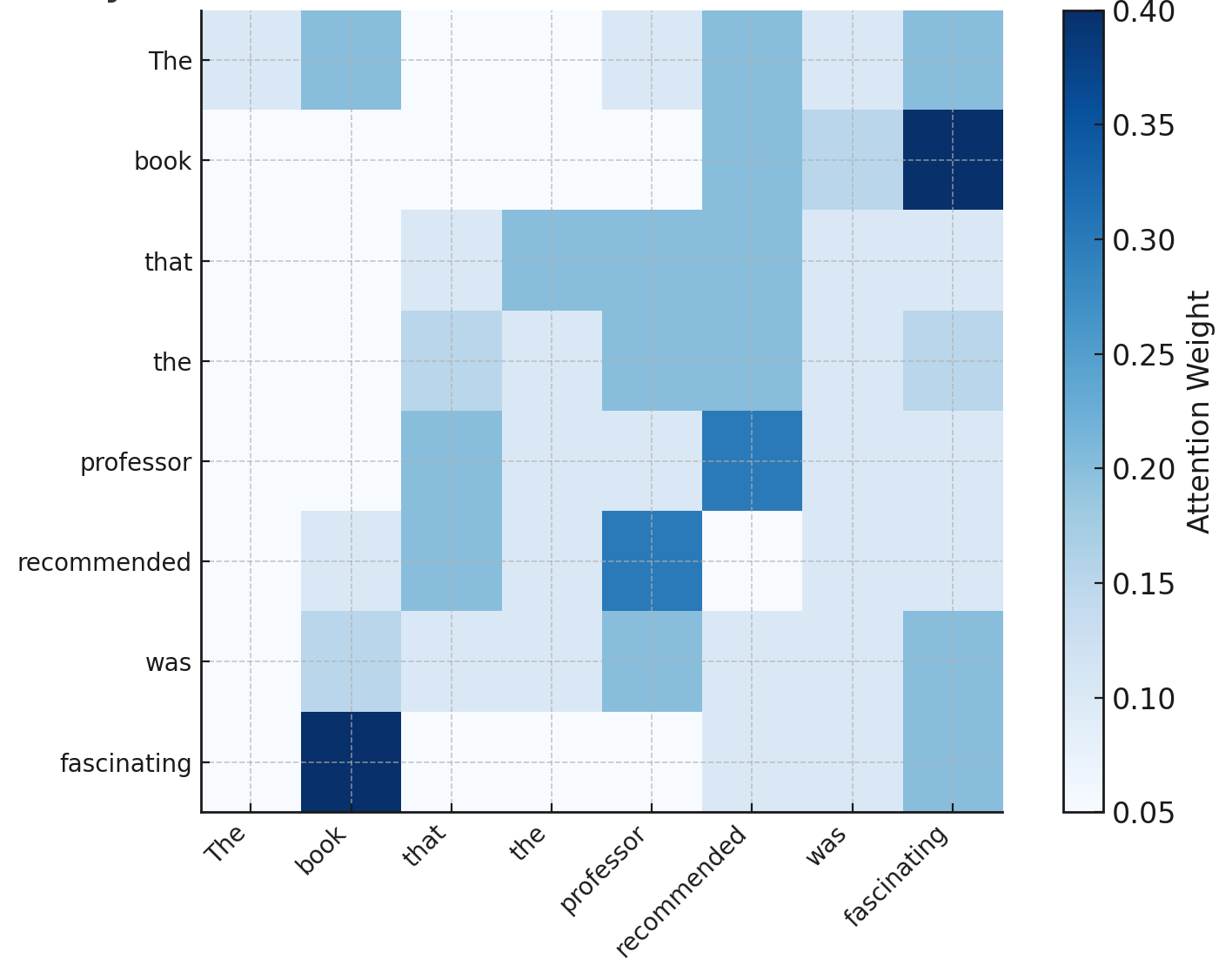
“The book that the professor who won the award recommended was fascinating.”
To make sense of this, you have to connect book to was fascinating, skipping over a detour about the professor and the award. Humans do this effortlessly. Early models did not.
The transformer, introduced in 2017, solved this problem with startling elegance. Its central innovation was attention. The model was named a transformer because each layer transforms raw embeddings into richer, context-aware versions of words. And because the architecture can transform one sequence into another, as in translation.
Figure 2. Toy schematic of a transformer. Input words are turned into vectors (embeddings). Each word then attends to the others (self-attention), producing context-rich representations from which the model predicts the next word. Stacking many such layers is what gives transformers their apparent fluency.
Rather than being trapped in a short memory window, attention lets the model look back over all previous words and decide which ones matter most. In the sentence above, when predicting fascinating, the model might give most of its weight to book, some to recommended, and very little to was or professor.
Figure 3. Toy attention map. When predicting “fascinating,” the model assigns greater weight to “book” than to intervening words like “professor” or “was.”
How Are These Weights Computed?
At the heart of a transformer is attention: a way of deciding, for each word being predicted, which earlier words matter most right now. Instead of treating all past words equally, the model learns to assign different weights.
It does this by giving every word two signals: a query (what it seeks) and a key (what it offers). The closer a query and key align, the more strongly the past word influences the current one.
Queries and keys aren’t assigned by hand. Each is produced by applying a linear function to the word’s embedding. Linearity here means something simple: the function preserves addition and scaling. If you add together two word-vectors and then apply the rule, you get the same result as applying the rule to each one separately and then adding the outputs.
Take a toy example. Suppose the embedding for cat is (2, 1). With weights (a, b), its query is a·2 + b·1. For dog at (1, 3), the query is a·1 + b·3.
What makes this rule linear is that it preserves structure. Add the embeddings for cat and dog, you get (3, 4). Apply the rule: a·3 + b·4 = (a·2 + b·1) + (a·1 + b·3). In general: addition and scaling commute with the rule.
Linearity isn’t just a mathematical curiosity; it’s what makes attention workable. A linear rule lets the model reshape the embedding space smoothly: stretching, rotating, or tilting it without destroying the relationships already encoded there. This stability means that patterns like cat and dog appearing in similar contexts remain comparable after transformation. It also keeps the mapping compact: a single set of weights can be reused across the whole vocabulary, instead of requiring a new nonlinear function for every word.
The crucial point: the weights (a, b, …) aren’t fixed. They’re learned parameters. Training nudges them until queries and keys highlight the relationships that make predictions accurate.
From Queries and Keys to Attention Weights
Once every word has a query and every previous word has a key, the model compares them. The comparison is a similarity score: if two arrows point in nearly the same direction, the score is high; if they diverge, the score is low.
Formally, multiply coordinates, add them up, get a number that measures alignment.
For the word being predicted, the query is compared to the keys of all previous words. That yields a list of scores, one per word. These scores are then converted into probabilities that sum to one.
High similarity → high probability (this word matters).
Low similarity → low probability (this word is mostly ignored).
The result is a set of attention weights: a distribution over past words.
It is a clever trick, but still a statistical one. The model can highlight relevance, yet it doesn’t ask why one word should matter more than another.
Alongside queries and keys, each word carries a value vector, the payload. Once weights are set, the model takes a weighted average of the values, producing a new, context-enriched representation of the word. In other words: queries and keys decide who matters to whom; values decide what information actually gets carried over.
How Attention Learns
But, for attention to work, the model must learn how to tune the linear functions that produce queries, keys, and values. Training provides the tuning.
Take a simple example: in the sentence, “The book was fascinating,” the model starts with a guess. Early on, it might focus too much on was and too little on book. From this initial guess, it assigns low probability to the correct word (fascinating) and high probability to others (boring).
The training process corrects this. The error signal tells it to boost attention to book and reduce attention to was. Over billions of such updates, the parameters that build the queries, keys, and values are nudged into place. Attention patterns sharpen: the right words consistently align, and fluent predictions emerge. Linearity is key here: it gives the training process a clear signal, aligning the queries and keys in a way that preserves the geometry of the embedding space.
But what does that feel like? A useful way to picture it is as a conversation. Each word has something to say, but it also listens, glancing around the table to decide whose voice matters most. A pronoun like it in “The animal didn’t cross the road because it was tired” gives most of its weight to animal, not road.
Crucially, this doesn’t happen step by step. Every word attends to every other at once. Each emerges with a context-rich version of itself, reshaped by what it has heard.
But this richness comes at a cost: if every word listens to every other, the number of comparisons explodes. The trick that made transformers feasible was parallelism: they process words all at once, spreading the load across many processors. This made scaling to billions of words possible.
Even so, attention has limits. Every transformer has a context window: a limited span of text it can attend to. Beyond that, the words don’t blur or fade; they simply vanish.
Yet even with this constraint, the transformer marked a decisive shift. What changed was not the objective—it still predicts the next word—but the architecture. By letting every word attend to every other in parallel, the architecture made prediction scalable and coherence stretch across pages. The breakthrough that brought us to machine fluency.
Back to the Question
We’ve seen how autoregression, embeddings, and attention make today’s language models astonishingly fluent. They are capable of coherence across paragraphs and able to mimic tone and form. Yet, their sentences flow without experience behind them.
But what about ours?
To see what is missing, we must turn from architectures back to ourselves—not to grammar, but to the generative process of a human mind.
The Loop of Human Expression
If transformers scale prediction through attention, writing scales meaning through struggle. The epics and masterpieces I grew up enact worlds of arguments, digressions, and layered truths. Their circular forms taught me that expression need not be linear to be profound.
Good writing is not just seamless continuation; it is the projection of thought into words and the fragile reconstruction of meaning in reading. Models see only finished sentences, never the hesitations or abandoned drafts that reveal a writer's judgment and what had to remain unsaid. A model never goes through that struggle. It can echo Shakespeare’s polish but it cannot create another Shakespeare, because it bypasses the refusals and revisions that give a voice its singular depth. To write well is to enter a loop of decomposition, discernment, and transformation between thought and experience, via language.
Some might object: doesn’t training on millions of texts already capture human experience? But meaning is not a mere average; it is anchored in a singular point of view. My unique lived experience anchors my words; another writer’s unique history anchors theirs. The machine blends these individual angles into a smooth, flattened composite—a statistical picture that can imitate any perspective, yet stands in none of them. Fluency, in this sense, is not the same as depth; it is a 2D rendering of a world that, for humans, is always 3D.
This problem runs deeper than simple averaging. The machine learns only from the finished products of our thought. It sees the seamless final draft, not the process that made it. Near-optimality in the space of weights is not near-optimality in the space of meaning or human experience. Even in the simpler setting of image classification, adversarial machine learning has shown how brittle models trained only on finished outputs can be; a tiny, imperceptible perturbation can flip a cat into a toaster. In language, where meaning is fragile and shifts with tense, tone, or a single word, the problem is infinitely harder.
This is why the gap is fundamental. We are robust precisely because our words are forged through lived judgment—through seams, hesitations, and revisions. These are not bugs, but the very sources of orientation and responsibility. Any system that aspires to be human-like cannot avoid them; it must, in some sense, live through its own seams.
The Human Loop
Let’s try to sketch, loosely, this internal loop. Like our earlier account of transformers, it is a simplification. But the contrast is revealing: it shows what these models do, and what they don’t.
Decomposition. The writer begins with an idea, intuition, or question, often large and indistinct. To express it, they must break it into smaller ideas and linearize them: which idea comes before the other?
Generation. Then writing begins. A sentence is produced for the first in the sequence.
Inner Experience. Now, the writer reads and feels. How does it land? Does it sound right? Is it true to the original impulse, or too much, too little, too soon?
Revision. Based on this felt sense, the sentence is reshaped. Or deleted. Or moved. This loop repeats: sentence by sentence, then paragraph by paragraph.
Structural Return. Often, the writer zooms out. Does the whole hold together? Are the parts accumulating toward something? Are they saying what they think they’re saying?
AI systems can assist with parts of this loop, but only after the idea has already been provided to them in the form of a prompt. In effect, the human does the first decomposition: deciding what matters and compressing it into an instruction the system can act on. From there, the machine excels at generation, producing fluent sentences on command, and it can sustain a degree of structural coherence within the boundaries of its context window. But the deeper steps remain out of reach. Inner experience—the felt sense of whether a line rings true—is absent. Revision is never self-initiated; it depends entirely on new feedback from the human, whose own experience supplies the standard of judgment. And structural return, the act of reframing a work against one’s own intention, lies beyond a system that has no intention to begin with. This recursive testing—drafting, deleting, reframing—is how a voice emerges.
Tacit Knowledge
This process depends on immense tacit knowledge: of tone, rhythm, genre, and audience, drawn from deep wells of memory and experience. Meaning shifts not just at the level of words, but at the level of frame. A writer may draft two very different openings to the same essay—one formal, one conversational—knowing each would change the direction of everything that follows. They may delete a whole section not because the sentences were wrong, but because the arc betrayed the deeper purpose. These choices emerge from lived judgment, not from probabilities.
A model, by contrast, treats alternatives as equally plausible. Take a prefix like “I don’t think he will ….” It might rate come, go, and stay as near-equivalents. All fluent. But only the writer knows if the moment calls for resignation, hope, or irony—and that choice reshapes the sentence and its place in the larger work. Transformers can echo the surface, but they do not feel their way through, or seek resonance. They simply continue.
When Agency Slips
What remains is a striking asymmetry: machines can continue, but only humans can decide what is worth continuing. And when we forget this, something else happens: the agency loop, which I described here. It begins with delegation and deepens with flattery, until revision itself is outsourced and judgment thins. What starts as help with the blank page ends with sentences that no longer feel one’s own.
In that loop, writing with a chatbot can feel like riding a horse with a mind of its own—the compressed mind of everyone. It moves fluently, sometimes beautifully, anticipating your direction, even surprising you. But the rider is never fully in control. What you’re steering is not just a model. It is a distillation of billions of sentences written by others, across time, genre, and culture. That’s its strength, but also its friction. You are not alone in the saddle. You are co-writing with the average, the archived, the dominant. This is the resistance many writers feel when trying to express something particular, personal, or strange.
The Mysteries That Remain
The path from Shannon and Turing to ChatGPT is a long march toward fluency. But in automating the statistics of language, something essential was left behind: the silence, the hesitation, the quiet struggle of a mind shaping thought into words. The models I saw that day were astonishing, but their seamlessness was the very thing that made them a mystery. They had no seams because they had no life to live through them.
The texts that shaped me carried power not in their words alone, but in the humanity behind them. A reminder that language is a living practice of agency and choice.
I was reminded of this earlier this year when I tried to write a tribute to one of the best teachers from my undergraduate days, who had just passed away. I wrote and rewrote the opening line for hours. Too formal. Too sentimental. Too flat. Eventually, I left it unfinished. Not because I didn’t care, but because I did. The words had to mean what I felt, and nothing quite fit. I couldn’t enter the state I needed: fully in grief, fully aware.
To write is not just to say something—it is to wrestle meaning into shape. Sentence by sentence, the writer listens inwardly: Does this ring true? Is this what I meant? I call this semantic friction: the struggle between what we feel and what we can say, like carving a curve into wood that resists the grain. That tension gives a sentence its gravity, and it is exactly what the machine bypasses.
A model can smooth a sentence, but it cannot feel the pause before a word or the jolt of truth when it lands. That day, over coffee and cake, I struggled to articulate what was missing in the student’s flawless summaries. I didn’t have the words then.
I do now.




Very well written and in simple language so that even a layman like me could understand that AI may perhaps never be able to grasp the spirit behind what is being written or being said
One thing I absolutely adore about Mr. Vishnoi's writing style is the simplicity. No use of jargons that really helps anyone to understand any concept he teaches.